工業技術研究院 資訊與通訊研究所 黃博煜 闕壯華

2023 Gartner 預測理論導引類神經網路技術(PINN) 在未來二至五年達到技術成熟期,目前國際研究單位紛紛投入相關應用研究。
前言
理論導引類神經網路技術(Physics-informed neural network, PINN)為近幾年興起的AI技術 [1],PINN 可以無縫地將資料和物理定律融入神經網路學習中,透過學理基礎來引導AI模型的訓練,打破過往AI模型需要收集大量實際資料才能學習的限制,加速模型開發及提高精準度。Gartner 2023年的 Hype Cycle for AI 也指出 PINN 是未來二至五年達到成熟期的AI技術之一,目前國際研究單位也紛紛投入相關研究,例如:Nividia, DeepMind, Berkeley, Stanford, Harvard, Cambridge,且涵蓋化工應用、航太應用、GPU 散熱設計、生醫、電腦圖學等應用領域。
精彩內容
1. PINN技術概論
2. PINN優勢與適用情境
3. PINN應用實績 |
技術概論
過往為了解一個現象的行為(如:彈簧簡諧運動)通常可由兩種方式來進行(如圖1),第一種是基於物基礎原理的方式來建立理論模型(Physical Model),並透過原理的計算,來描述出變數間存在的關聯性。另一派計算機科學的學者,則是以數據模型(Data-driven Model)的方式來處理,透過收集大量的資料,利用數學模型(如:類神經網路模型)由資料中自動學習出變數間的對應關係。雖然理論模型準確度相當高,但這樣的做法高度仰賴領域知識,建立時也需要耗費大量時間,且對於無法用完整的理論描述或以及理論與實際有所差異之應用,預測準確度仍有偏差;數據模型則是需要夠多的資料才會有不錯的預測效果,此外無解釋性以及不容易處理外插預測也是數據模型在實務運用的一大限制。

圖1 PINN 技術概念圖
然而 PINN 試圖將理論方程式與資料融入一個類神經網路模型中(如圖2),讓模型可同時學習理論方程式的特性以及資料的關聯性行為,其方式是將理論方程式導入類神經網路模型的損失函數(Loss Function),在模型訓練時不僅要讓預測值與真實值的誤差愈小愈好(如:資料損失函數為平均平方誤差),也讓模型預測結果盡可能滿足理論方程式(如:方程式損失函數為方程式等號兩端之平方差值),因此整合資料損失函數及方程式損失函數後,PINN 模型損失函數可表示成
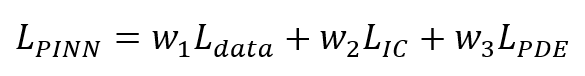
其中Ldata為資料的損失函數(等同於傳統類神經網路模型的損失函數,若以平均平方誤差損失函數可表示為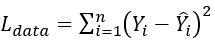 ,Yi 為實際值,Y ^i 為預測值)並可透過實際資料的蒐集(ti,Yi)來計算;LPDE為方程式損失函數,若以簡諧運動理論方程式的平方誤差損失函數為例,可表示為
,Yi 為實際值,Y ^i 為預測值)並可透過實際資料的蒐集(ti,Yi)來計算;LPDE為方程式損失函數,若以簡諧運動理論方程式的平方誤差損失函數為例,可表示為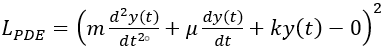 ,可生成多個參數評估點(如:t在0~10中的等分切割1000個格點值),並透過自動微分法(Automatic Differentiation,AD)計算;LIC為初始條件損失函數,在簡協運動理論方程式中,初始平方誤差損失函數可表示為
,可生成多個參數評估點(如:t在0~10中的等分切割1000個格點值),並透過自動微分法(Automatic Differentiation,AD)計算;LIC為初始條件損失函數,在簡協運動理論方程式中,初始平方誤差損失函數可表示為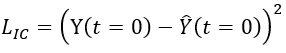 ;w1, w2, w3為整合權重。
;w1, w2, w3為整合權重。
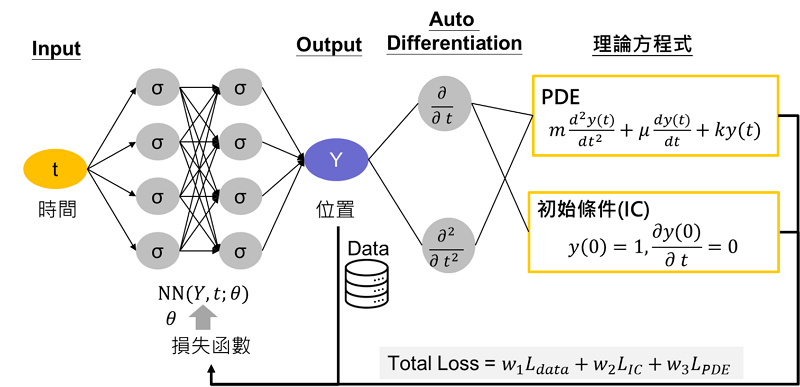
圖2 PINN 模型架構圖
當模型同時考慮資料損失函數及方程式損失函數時,可以確保模型的預測值(如圖2的Ŷ)不但可以貼近訓練資料集(資料損失函數,如圖2的Ldata),也可以符合理論方程式(方程式損失函數,如圖2的LIC及LPDE),因此可提升模型在預測應用的可信度(避免完全仰賴數據集來進行模型訓練可能造成的樣本代表性偏誤問題),但由於 PINN 是整合多個損失函數,每個損失函數的特性皆不盡相同,容易出現模型訓練收斂性不佳的現象,例如在模型訓練中在反向傳播演算法(Backpropagation)時會發生梯度不平衡(Gradient Imbalance)的現象,疊代更新會集中在特定損失項上,而造成某些損失項無法收斂。此外,透過大量生成的虛擬樣本點來進行模型參數的訓練,也容易出現模型訓練收斂性延遲的現象,例如在高維方程式的應用中虛擬樣本點數量相當龐大,而隨機批次選擇訓練樣本時,則可能很高機會選擇到無梯度資訊的樣本,而導致延遲收斂。因此 PINN 的收斂性仍是未來一個很大的技術挑戰。
技術優勢與適用情境
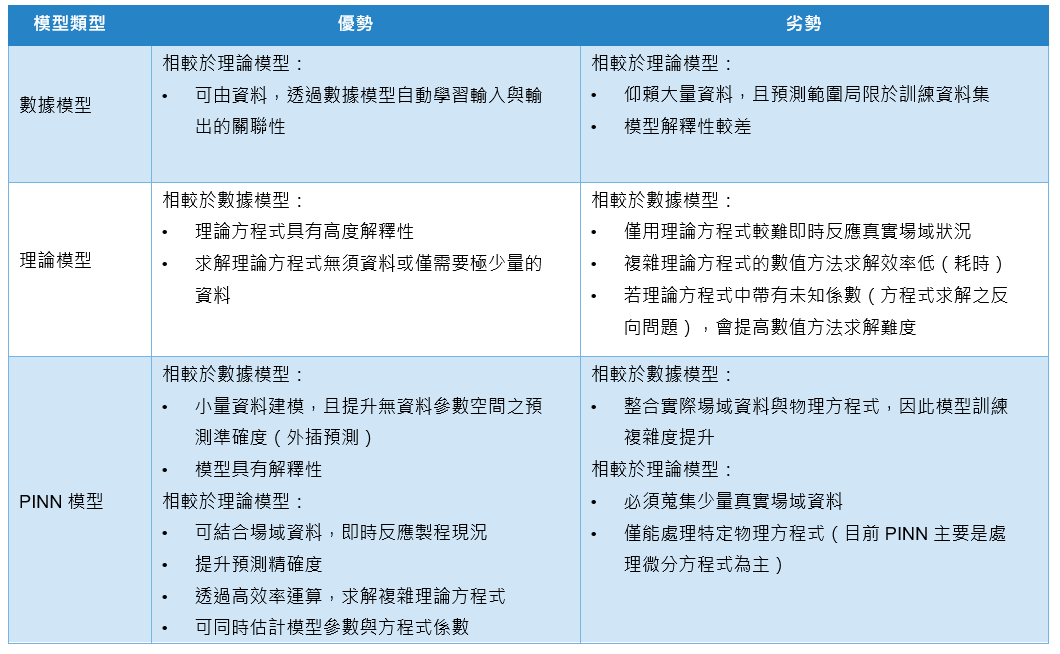
目前 PINN 處理的理論方程式是以微分方程式(Differential Equation)為主,例如化工反應動力學或震動理論的常微分方程式(Ordinary Differential Equation, ODE)、固體力學或流體力學理論的偏微分方程式(Partial Differential Equation, PDE)、動態系統或隨機過程的隨機微分方程式(Stochastic Differential Equation, SDE),而 PINN 相較於傳統數據模型(如:類神經網路模型或機器學習模型)或理論方程式數值解方法(如:有限元素法或有限差分法)的差異與優勢在於(1)提高預測準確度:結合理論模型及少量資料,可即時反應資料現況,建立高精準度的預測模型,並適用於訓練資料未涵蓋之參數空間的預測(外插預測);(2)快速求解理論方程式:解決現有數值解法計算量時間長的問題,透過 PINN 的高效率計算的方式,可做為複雜理論方程式的求解器;(3)同時解決理論方程式的正向與反向問題:PINN 可同時估計模型參數與方程式之未知係數,縮短模型開發之時程;(4)發覺或確認理論方程式:利用 PINN 模型可確認或發掘新的理論方程式。表1整理數據模型、理論模型以及 PINN 模型的優缺點。
表1 數據模型、理論模型以及 PINN 模型的優缺點比較分析
目前國際大廠及研究單位也紛紛投入相關研究,例如:NVIDIA 所開發的 Modulus 則是以 PINN 為架構的數位雙生平台,西門子能源(Siemens Energy)使用該平台並應用於鍋爐的預測性保養維護來減少停工頻率及增加生產效率;而西門子歌美颯(Siemens Gamesa)也運用 PINN 技術來快速計算流體力學方程式,模擬高解析度的風場變化,提高風機發電效能。此外 DeepMind 也透過結合數據及數學限制式來訓練 PINN 模型,用於求解複雜的量子化學問題,可精確估測材料屬性,其相關成果也發表於 Science 期刊。
應用實績
石化產業製程品質預測:減少訓練資料量及提升預測準確度
石化產業在數據建模時,經常會面臨少量資料的議題(品質量測取樣頻率低,較難收集大量數據),而導致模型準確度不佳的情況。因此本案例導入 PINN 建模技術,結合化工製程理論公式(製程化工反應動力學的ODE方程組)及少量工廠數據,經驗證測試後,相較於單純數據模型,PINN 模型不僅可減少50%以上的訓練資料量,也降低預測誤差79%(產品品質預測絕對誤差由0.064下降至0.014),加快模型上線使用時程,且由於此模型具有良好的外差預測效能(無現場操作數據的參數空間,其預測值仍遵循理論法則),因此可透過製程操作參數的優化推薦來改善製程品質。
散熱設計中模擬計算:加速模擬計算速度
在許多設計優化的應用中,大多仰賴模擬器來評估設計方案的優劣,模擬器中求解理論方程式的方法為數值求解法,其運算時間較長且不同設計方案皆需要重新模擬計算,因而影響設計優化的效率,本案例則使用 PINN 技術,充分運用 GPU 運算優勢,加速理論方程式的求解速度,並可推論任意參數空間。在整合熱傳導(克希荷夫定律)與熱對流(牛頓冷卻定律)理論方程式的散熱應用中,PINN 求解法與有限差分數值求解方法相比,在平均絕對百分比誤差為0.025%下,計算時間可加快100倍以上,並可將散熱設計變數納入 PINN 模型中,以加快設計優化之效率。
結論
PINN 結合理論知識與資料學習的創新做法,已經在許多產業應用陸續得到實證,例如設計優化、製程改善、模擬加速,但是在核心技術面上,整合更多個的損失函數所導致的模型的收斂性問題,以及牽涉更複雜理論方程式的多重耦合應用仍需要持續改善與精進,此外 PINN 的相關概念如何鏈結到生成式人工智慧(Generative AI, GAI)之相關應用的也可能是另一個突破重點。
參考文獻
[1]Karniadakis, George Em, et al. "Physics-informed machine learning." Nature Reviews Physics, vol. 3, no. 6, pp. 422-440, 2021.
[2]Wang, Sifan, Yujun Teng, and Paris Perdikaris. "Understanding and mitigating gradient flow pathologies in physics-informed neural networks." SIAM Journal on Scientific Computing, vol. 43, no. 5, pp. A3055-A3081, 2021.
[3]Willard, Jared, et al. "Integrating scientific knowledge with machine learning for engineering and environmental systems." ACM Computing Surveys, vol.55, no.4, pp.1-37, 2022.
[4]Wu, Chenxi, et al. "A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks." Computer Methods in Applied Mechanics and Engineering, vol. 403, pp.115671, 2023.
[5]https://resources.nvidia.com/en-us-energy-utilities/siemens-gamesa-wind
[6]https://resources.nvidia.com/en-us-energy-utilities/siemens-energy-nvidia
[7]Kirkpatrick, James, et al. "Pushing the frontiers of density functionals by solving the fractional electron problem." Science, vol 374(6573), pp. 1385-1389, 2021.