工業技術研究院 資訊與通訊研究所 劉志尉 李佑荃

卷積式神經網路（convolutional neural network, CNN）是目前應用最廣泛的神經網路。典型的CNN主要由不同形式的運算層所構成，其中包含卷積層（convolutional layer）、池化層（pooling）、非線性整流層（rectifier linear unit, ReLU）、完全連接層（fully-connected layer）、以及歸一化函數層（softmax）等。

這些不同類別的運算層所構成的深度階層式架構，可讓CNN將輸入資料轉化為不同深度含意的特徵（feature），再藉由不同特徵特性的非線性計算，達到影像辨識、視訊分析、自然語言處理、或新藥物發現等目的。卷積層的運算等效於一特定的矩陣乘法運算，是CNN中運算量最高的運算，有時會超過全部的90％。

Systolic Array是一種通用矩陣乘法加速器，因其具有規律與高度平行運算的優點，因此多數大廠或研究單位，如NVIDIA Tensor Core、Google TPU、Eyeriss I/II、ShiDianNao系列、Chain-NN、Cambricon-x等，均採用Systolic Array來進行AI晶片的設計。

雖然Systolic Array可簡化內部乘-累加器（multiply-and-accumulate, MAC）或處理單元（processing element, PE）之間的資料傳遞，但另一方面，Systolic Array在實現稀疏與非規則矩陣乘法運算時會有低硬體使用率、記憶體空間浪費等問題，過多的能量損失將導致終端裝置的使用時間大幅縮短。因此，如何有效的處理與實現稀疏與非規則矩陣乘法運算是次世代AI晶片亟需解決的問題。

精彩內容 1. Systolic array、CNN、稀疏與非規則矩陣乘法運算 2. 高效能稀疏與非規則矩陣乘法運算加速器架構 3. 同時可支援INT8與BF16格式之多輸入多輸出乘法陣列與樹狀形累加器設計

CNN與矩陣乘法運算

圖1(a)顯示CNN中的卷積層的運算過程。若我們將圖1(a)中的二維filters以一維（1D）row的形式展開，並將其對應相乘的input data子區塊以一維column的形式展開，再分別將row filter與column data組成如圖1(b)中的"Filter matrix"以及"Data matrix"，如此，卷積層運算即等效於一矩陣乘法運算（GEMM）［1］。

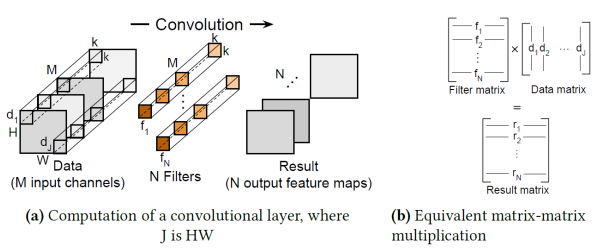
圖1 Computation of a convolutional layer and its equivalent GEMM [1]

Systolic Array [2] 因具有規律與高度平行運算的優點，可以最高的能量效益實現具低功耗與高吞吐率特性的通用矩陣乘法加速器，因此，目前CNN加速器主要結構均Systolic Array為主。在CNN的推論與訓練運算中，每一卷積層中的Input feature map共用同一組filter kernels，因此，在進行運算前，我們會先將Filter matrix（或稱為Stationary matrix）加以儲存，而後依次將不同的Data matrix（或稱為Streaming matrix）輸入，經過Systolic Array計算後即可完成卷積層的運算。值得一提的是，為了滿足Systolic Array同步的要求，其輸入與輸出必須是skewed矩陣形式。

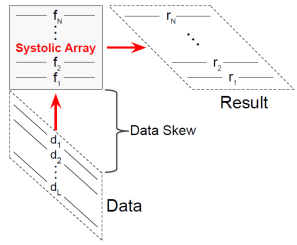
圖2 Weight-stationary systolic array [1]

為了降低CNN運算複雜度，設計者常使用weight pruning技術，即在CNN的訓練與推論過程中，將不重要的係數、或較小的係數刪除（即以0取代），而不會影響物件分類與辨識準確率。以VGG-16為例，如圖3所示，weight pruning技術可將原先網路中40％~80％係數刪除；另一方面，神經網路中的ReLU運算，會使得多數的output數值為零。同樣以VGG-16為例，經過ReLU計算後，Output feature map有20％～70％中的數值為零。如此一來，VGG-16各卷積層中約有40％～90％以上的無效（ineffective）MAC運算。

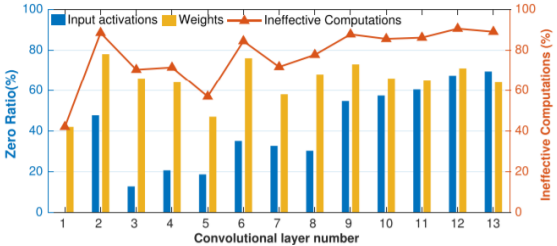
圖3 Ineffective computations analysis due to zero operands for VGG-16 [3]

雖然Systolic Array可有效實現方陣矩陣乘法，但在實現非規則矩陣乘法以及稀疏矩陣乘法運算時，Systolic Array效率變差。為了方便說明，我們以一4x4 Systolic Array為例，如圖5所示，來分別實現圖4中規則的、非規則的、以及稀疏的矩陣乘法[4]。為了比較，圖4中不同形式的A（MK）B（KN）運算中其Stationary matrix B的非零元素都是16個，亦即3個不同的矩陣乘法所需的總乘法數相同。

圖4 不同形式的GEMMs [4]

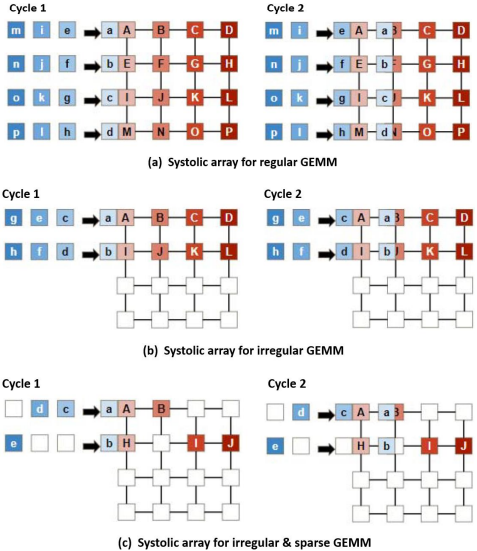
圖5 Systolic array for variant GEMMs [4]

首先我們將圖4(a)中4x4方陣B存入Systolic Array，接著將方陣A輸入，如圖5(a)所示，利用7個cycles即可將4x4方陣乘法的結果計算出來。為了製圖方便，我們省略skewed matrix的形式，僅以示意圖來描述Systolic Array的運算過程。但對於圖4(b)中的非規則矩陣乘法例子來說，因為4x4 Systolic Array無法一次將2x8矩陣輸入，我們必須將其切成2個2x4子矩陣，再分成2個回合來執行，如圖5(b)所示。同理，對於圖4(c)中的2x10稀疏矩陣來說，我們必須將其切成3個子矩陣，分成3個回合來執行，如圖5(c)所示。Systolic Array在實現圖4(a)方陣乘法運算時，其PE的使用率為100％，但對於圖4(b)的非規則矩陣乘法而言，其PE使用率僅達50％，而且需要2個回合來計算，如果不計I/O Buffer間的延遲，共需14 cycles才能完成計算。圖4(c)的稀疏矩陣乘法其PE的使用率更低，3個回合的PE使用率分別為31.25％、43.75％、以及25％，且共需21 cycles才能完成計算。

低硬體使用率對於系統效能的影響為何?我們以參考論文[4]所舉的例子來做說明。Google tensor core V100配置數量龐大的MACs，其FP32以及FP16浮點數運算效能分別15.7 Tflops/s以及125 Tflops/s，如圖6(a)中的藍線與紅線所示。但若我們利用各種不同形式的非規則矩陣乘法來測試，V100所實測的FP32以及FP16浮點數運算效能降為12 Tflops/s以及82 Tflops/s的。更糟的是，對於稀疏且非規則矩陣乘法，V100的效能更低，所測得的FP32運算效能已經不足4 Tflops/s。

圖6 Google tensor core performance evaluation on different GEMMs

因為功率考量，現有用於終端設備的AI加速器多數採用定點數INT8的資料格式，但常用的CNN/DNN開發環境，如TensorFlow、PyTorch等，仍以浮點數FP32的資料格式為主。一個已訓練完成的FP32 CNN模型，無法輕易地移植到定點數INT8的AI加速器中，需要多次、耗時的quantization aware training（QAT）過程。雖然QAT技術可將FP32的係數以較低精確度的資料型態表示並進行運算，但隨之而來的是CNN辨識準確度降低，已經有越來越多的CNN應用顯示，INT8資料格式的乘法與加法器已不符所需。為了解決這個問題，近年來Google Brain提出了一種新型的資料型態：Brain Floating Point（BF16）。

BF16與FP32資料型態的比較如圖7所示。若將FP32的fraction（或mantissa）部分中的後16位元移除，FP32即變為BF16格式，反之，將BF16中的fraction部分補16個0，BF16即變為FP32格式。換言之，BF16與FP32兩者格式之間的轉換容易，只是BF16格式有較低的精確度（precision），但BF16的總長度為16位元，所需的記憶體空間與記憶體頻寬較小。BF16保持與FP32相同的指數型式，因此兩者有相當的動態範圍。在進行運算時，捨去指數部分後，BF16保留sign與fraction後剛好為8-bit，此與INT 8的格式相仿，因此在架構上，BF16與INT8格式容易整合。目前Nervana、Xeon、Intel、Google、TensorFlow、ARM、AMD、NVIDIA CUDA等都已採用BF16，因此同時能支援BF16與INT8資料型態的AI加速器將是未來的主流。

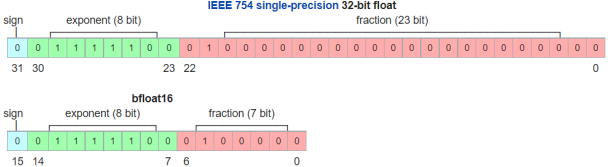
圖7 BF16與FP32資料型態比較圖
 

稀疏與非規則矩陣乘法運算加速器

如前所述，AI加速器需處理大量sparse & irregular GEMM。一般AI加速器中的記憶體空間有限，無法將所有Input feature maps、weight matrices、以及output feature maps都儲存於內部記憶體中，因此常見的處理方式會將intermediate value（或partial sums）儲存於外部記憶體中。因此如何處理sparse matrix資料儲存與搬移，是AI加速器必須解決的問題。常見的解決方式是採用matrix壓縮格式，例如CSR（compressed sparse row）、CSC（compressed sparse column）、COO（coordinate format）等，另外還有RLC（run-length compression）方式。

RLC方法是一種紀錄數值的重複次數作為表示的一種壓縮方法，例如一個數列[2, 2, 2, 2, 2, 7, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 2, 2]，經過RLC壓縮之後，可記錄為[2, 5, 7, 1, 0, 10, 1, 2, 2, 2] （註：為了方便讀取，上述RLC格式中的黑粗體字代表重複次數）。COO格式是將matrix中非零值以矩陣座標的方式儲存，因此除了儲存矩陣中非零值之外，還要儲存row-index vector以及column-index vector。假設一稀疏矩陣如下所示：

利用COO儲存，其所儲存的格式如下：

CSC格式類似CSR格式，在此就不做贅述。在CNN的應用中，輸入與輸出的矩陣有越來越大的趨勢，可從32x32到1024x1024，未來可能將處理8K Image。矩陣格式越大，其col-index/row-index所需的位元數也需增大。概括來說，COO/CSR/CSC所需的空間大約是稀疏矩陣中非零值總數的三倍。

一種更有效率的稀疏矩陣壓縮格式稱為Bitmap表示法[4]。顧名思義，Bitmap表示法是利用1-bit的矩陣格式來表示矩陣中非零數值的位置。以前述的稀疏矩陣為例，其Bitmap表示法如下：

圖8為各種不同稀疏矩陣壓縮格式效率的比較[4]］。若以MxK矩陣為例，其中M=1632、K=36548，矩陣的稀疏性從10％變化到90％。如圖8所示，因COO/CSR/CSC等需額外的高位元index vectors，因此矩陣的稀疏性要夠高，例如>50％，其壓縮的效能才會展現出來。當稀疏性接近90％時，2-bit RLC或4-bit RLC的壓縮效果最好；但是，當壓縮率僅有30％（或更少）時，RLC的資料量會略高於Bitmap表示法。RLC雖然有不錯的壓縮表現，但其最大的缺點是無法直接進行運算，必須將其還原回原矩陣才能進行運算。反觀，整體來看，Bitmap的壓縮效果表現都十分優異，而且Bitmap表示法保有原矩陣的型態，透過Bitmap可以直接進行運算，這在產生控制訊號時有很大的幫助。

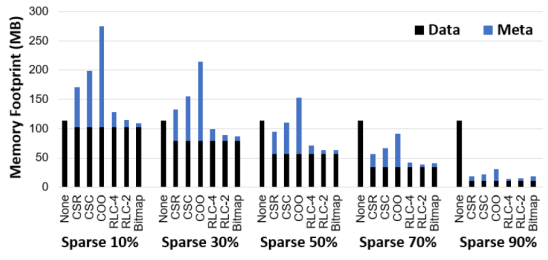
圖8 Matrix memory overhead with different compression format

 

目前文獻中已有多種矩陣乘法運算加速器的設計，其架構的比較如表1所示。

表1 多種稀疏矩陣乘法加速器的效能比較

其中，Packed Systolic-array[1]需要搭配軟體，並對原 Systolic Array 架構作大幅修改； SpArch[5]採用 outer product 矩陣乘法技術；MatRaptor[6]則採用 row-wise product 矩陣 乘法技術；而 SIGMA[4]採用 dot-product 矩陣乘法技術（限於篇幅，我們無法一一詳細 介紹。有興趣的讀者，可參閱參考論文）。從表 1 可看出，對於稀疏矩陣運算，SIGMA 有最好的 Efficiency Throughput。

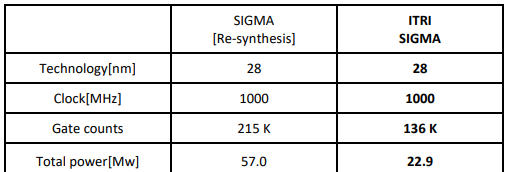
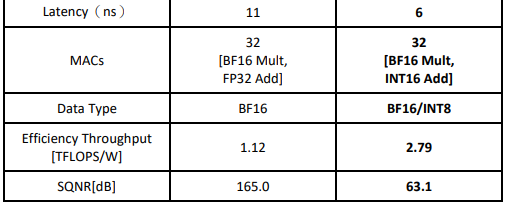
在深入了解 SIGMA[4]的架構後，我們發現作者在設計時以 4x4 小矩陣為例，導致 原 SIGMA 內部資料流在處理較大矩陣時會產生碰撞（Conflict）的問題；另一方面，SIGMA 採用 BF16 乘法器以及 FP32 加法器，雖可提供非常高的運算精確度，但也損耗大量的 Dynamic Power。

在 AI-on-Chip 計畫中，我們修正了 SIGMA 架構的缺點，並加以優化，同時為了低功 率需求，我們設計一特殊多輸入與多輸出的融合乘-累加器單元，使之能同時支援 INT8 與 BF16 兩種資料格式。為了公平起見，我們重新實現（Re-Synthesis）SIGMA 並與之比 較。表 2 為實現數據與比較結果。我們所設計的 ITRI SIGMA 優於原架構，唯一不足的是 運算精確度。ITRI SIGMA 提供的 SQNR 約為 63.1 dB；而原架構的 SQNR 約為 165 dB。

 

表2 所設計的ITRI SIGMA與state-of-the-art架構比較

 

雖然 ITRI SIGMA 其 SQNR 僅達 63.1 dB，但卻不會對 CNN 的辨識準確率造成影響。表 3 為參考論文[7]所得的比較數據。該論文提出一種低精確度之算術單元，稱為 Mitchell’s approximation arithmetic unit，簡稱 Mitchell 算術單元。Mitchell 算術單元所提供的 SQNR 更低，只有 46 dB [7]。但從參考論文[7]中的模擬數據顯示，對於多個常使用的 CNN 模 型，FP32 與 BF16 的辨識準確率幾乎相等。與 BF16 相比，Mitchell 算術單元其準確率幾 乎都維持相當的準確率，只有在 MobileNetV2 會下降大約 2.8％。因此，我們所提的 ITRI SIGMA 可滿足現有 CNN 的應用。

 

表3 不同計算精度對於多種CNN模型的準確度效能比較[7]

 

INT8/BF16融合乘累加器設計

我們所設計的ITRI SIGMA架構示意圖如圖9所示，其中包含3個部分：（1）multiple-input O（1）crossbar distribution network；（2）1D-array BF16/INT8 multipliers；（3）multiple-output adder-tree based BF16/INT8 reduction network。

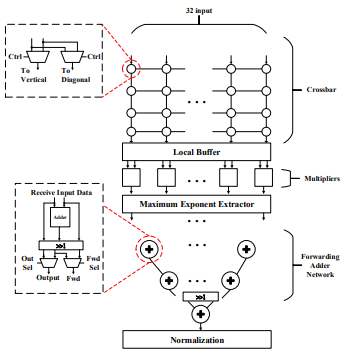
圖9 Proposed dot-product engine（DPE）for sparse & irregular GEMM

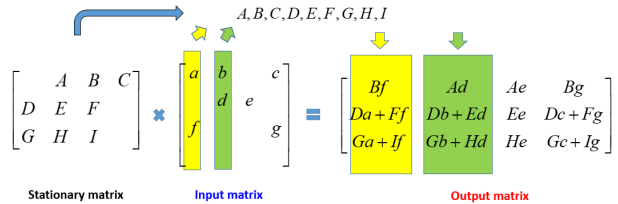
圖10 Illustrated example of sparse GEMM for SIGMA

有別於2D平面型式的Systolic Array，我們將矩陣乘法拆解為多個1D型式的dot-product運算。針對如圖10的矩陣乘法，首先我們將Stationary matrix的非零值，也就是（A, B, C, D, E, F, G, H, I），儲存於圖9架構中local buffer。接著依次將圖10中input matrix的column輸入。第一次輸入的column為（a, 0, f, 0）^T，透過crossbar network，僅需一個cycle可將a, f傳送到需與之相乘的乘法器中，亦即（-, f, -, a, -, f, a, -, f），其中”-“代表0。經過一維乘法器陣列的運算，可得

（A, B, C, D, E, F, G, H, I）x（-, f, -, a, -, f, a, -, f）=（-, Bf, -, Da, -, Ff, Ga, -, If）

隨後將所得之（-, Bf, -, Da, -, Ff, Ga, -, If）利用adder tree的相加運算，可以分別把Output matrix的每一個column數值計算出來，亦即（Bf, Da + Ef, Ga + IF）^T，此即為output matrix的第一個column。相同的，當輸入圖10中input matrix第二個column後，經過multiple-input, multiple-output（MIMO）DPE運算後，可得output matrix的第二個column；以此類推，便可完成sparse GEMM的運算。

我們所設計的ITRI SIGMA具有以下的特點：（1）具可擴充性架構。多個架構可組成一個大的SIGMA Engine；（2）利用reduction-tree累加器，ITRI SIGMA僅需log₂N cycles即可完成N個數值的累加；（3）ITRI SIGMA可執行任意維度、任意形式的矩陣乘法運算；（4）因為只進行非零值的運算，所設計的ITRI SIGMA可提供較高之effective throughput；（5）利用Bitmap壓縮技術，ITRI SIGMA所需的記憶體空間與記憶體頻寬較低；（6）ITRI SIGMA同時支援定點數INT8以及浮點數BF16矩陣乘法運算。

圖11展示我們所提出之INT8/BF16多輸入、多輸出融合乘累加器設計，其中Forwarding Adder Network如圖12所示。限於篇幅，我們省略詳細的運作說明。

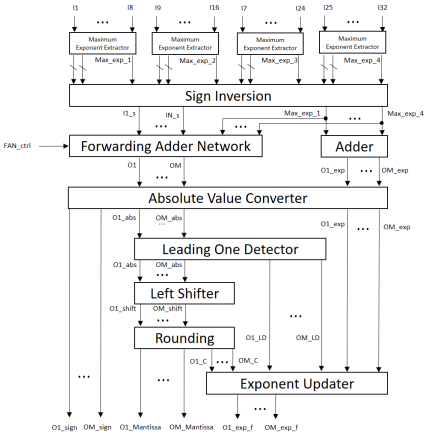
圖11 Proposed MIMO BF16/INT8 fused MAC（FMAC）unit

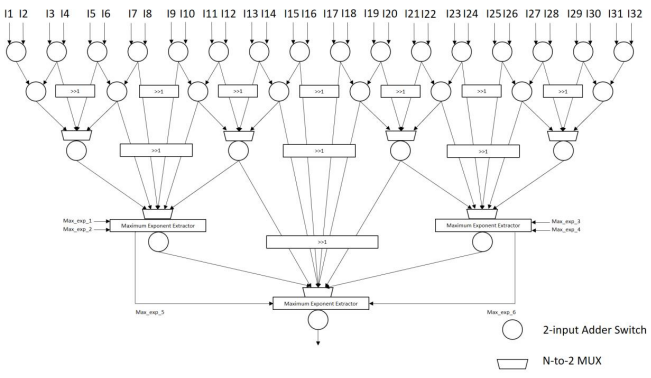
圖12 Proposed multiple-output adder reduction network

 

結論

我們所設計的ITRI SIGMA為一種新型AI加速器結構，具有高頻寬效益且具可擴充性，除通用的方振乘法外，ITRI SIGMA可有效率的處理不規律且稀疏矩陣乘法，達到高效能、低功率損耗的AI加速器目的。

參考資料

[1] H.T. Kung, B. McDanel, and S.Q. Zhang, “Packing sparse convolutional neural networks for efficient systolic array implementations: column combining under joint optimization,” in ASPLOS, Providence, April 2019
[2] H. T. Kung, "Why systolic architectures?" IEEE Computer 15, Issue 1, pp. 37–46, 1982
[3] J. Li et al., "SqueezeFlow: A sparse CNN accelerator exploiting concise convolution rules," IEEE Trans. Comput., vol. 68, no. 11, pp. 1663-1677, Nov. 2019.
[4] E. Qin et al., "SIGMA: A sparse and irregular GEMM accelerator with flexible interconnects for DNN training," in HPCA, San Diego, April 2020
[5] Z. Zhang, H. Wang, S. Han and W. J. Dally, "SpArch: Efficient architecture for sparse matrix multiplication," in HPCA, San Diego, 2020
[6] N. Srivastava, H. Jin, J. Liu, D. Albonesi and Z. Zhang, "MatRaptor: A sparse-sparse matrix multiplication accelerator based on row-wise product," in MICRO, Athens, 2020
[7] H. Kim, “A low-cost compensated approximate multiplier for Bfloat16 data processing on convolutional neural network inference,” ETRI Journal, vol. 43, pp. 684-693, February 2021.