工業技術研究院 資訊與通訊研究所 魏瑋辰 盧峙丞 林晉宇 莊凱翔 鄭桂忠

基於記憶體內運算的硬體規格的條件下，提出極小讀取邊際問題，並使用重新參數化技巧結合的機率模型，改進ADC量化器，能有效應用於多位元記憶體內運算的硬體。

記憶體內運算電路（IMC）在仿神經網路計算方面展現極佳的潛力，本文考量類比混合運算於非揮發性記憶體內運算（nvIMC）的硬體限制，提出基於Concrete分布的量化方法，用來優化在類比混合運算的變異引起的最小讀取邊界問題，使得模型能有效應用於非揮發性記憶體內之類比混合運算晶片系統。

研究背景

記憶體製程隨著摩爾定律逐年趨緩，記憶體的能源效率隨之飽和，具大量參數的深度學習模型使得資料反覆在記憶體層與處理單元間進行讀寫及計算，而這些晶片內部的層間資料會造成整體系統在信息傳遞上消耗大量能源，並受限於輸入及輸出匯流排的傳輸速度，也就是所謂的“馮紐曼瓶頸” （von Neumann bottleneck），而透過記憶體內運算可以打破記憶體牆限制[1]，其具備以下優勢:1)參數儲存於記憶體運算架構，避免資料傳輸的延遲;2)矩陣向量乘法計算透過交叉狀架構處理;3)減少MVM計算時晶片內部的層間資料數量。
記憶體內運算受益於打破馮紐曼瓶頸受到注目，然而，在[2]中，提出在nvIMC運算模式下開啟字元線（Word Line, WL）會累加出大電流並增加感知放大器的偏差，從而導致轉換錯誤。本文將此問題稱作“極小讀取邊際問題（Small Read Margin Problem, SRMP）”，當使用多位元的RRAM-based nvIMC時，此問題變得更加嚴重[3]，本文提出一種量化準則，並解決了nvIMC的硬體限制及極小讀取邊際問題。

硬體限制

本文著重於考量在nvIMC之多位元類比感知放大器的精確度以及極小讀取邊際問題的深度神經模型壓縮方式，本章節介紹了關於網路量化方法，並且介紹記憶體內運算的概念以及其硬體上的限制，最後詳細介紹欲解決的問題。

• 量化神經網路

考量到深度神經網路所需大量的資料計算集儲存空間，模型量化演算法備用來壓縮模型大小集計算量，如圖1(a)所示，模型量化主要會有兩個面向:權重量化以及激勵函數量化，權重量化能大量的減小模型儲存空間，而激勵函數量化能減少計算空間以及計算量。

• 非揮發性記憶體內運算

非揮發性記憶體內運算受益於可將網路權重預先儲存至記憶體單元內，透過特殊設計的運算電路達到記憶體內的卷積運算，藉此避免傳統馮紐曼架構裡記憶體間大量資料搬運，本文以1T1R單級單元（Single Lebel Cell, SLC)的RRAM與二位元深度神經網路(Binary Neural Network, BNN），講解記憶體內運算如何實踐加速運算如圖1(b)。
首先，對網路權重w移植記憶體內運算電路，透過設定記憶體單元處於低阻態（Low-Resistance State, LRS）或高阻態（High-Resistance State, HRS）來代表二位元之＂1＂或＂0＂。第二步，將量化網路的二位元激勵函數的數值作為記憶體的字元線是否輸入電壓之依據。如果激勵函數為零值，則字元線不會輸入任何電壓。若激勵函數有值，則記憶體單元會依據Kirchhoff定律，產生對應單元阻態的單元電流。第三步，透過將多個單元電流在記憶體位元線上累加得到位元線電流。最後，將位元線電流通過良好設計的ADC轉換成數位形式的二位元數值輸出，作為神經網路的下一層輸入訊號。

• 極小讀取邊際問題

對於多精度RRAM-based IMC設計仍有許多挑戰，一是位元線上的累加電流分布會在大電流的區域時，分布區間過小或重疊，導致DNN的模型準確率降低，圖1(c) 表示了基於測量高阻態與低阻態的MAC值得BL電流分類分布，當MAC輸出較小時，分類分布的邊際有一定距離，因此ADC將小電流轉換為數位數值可以分得很清楚，然而當BL電流變大時，ADC可能因讀取邊際變得極窄，轉換成錯誤的相鄰值，導致MAC輸出不再是由權重及激勵函數決定的固定值，而可能在取樣過程產生機率性。

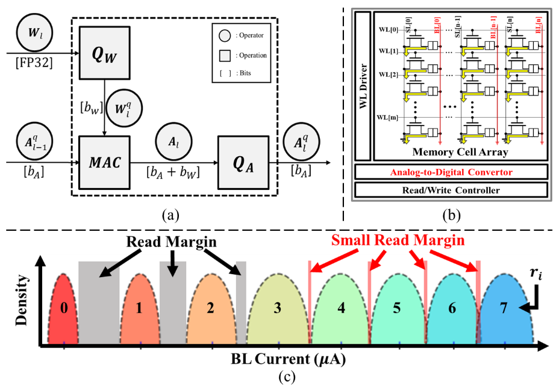
圖 1 (a) 一般網路量化的計算圖; (b) 1T1R的RRAM架構; (c) 極小讀取邊際問題

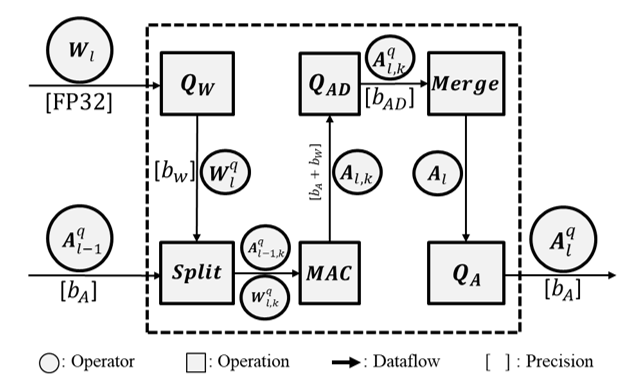
圖 2 所提出的模型訓練架構計算圖

記憶體內類比混合運算量化準則

• 基於Concrete分佈的ADC量化器

前文提出了極小讀取邊際問題（SRMP），以蒙地卡羅法模擬BL的電流數值分佈，透過不同的WL開啟數量及BL權重數值組合，獲取每個分佈的最大值、最小值與累積數據，在ADC量化器的設計中，引進了兩個可訓練參數:放大因子與偏差因子 ，透過這兩個參數能建構一個可學習的代表位階　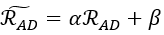，其中 等同於ADC量化器代表位階， 基於上述設定，將關於感知放大器  的假設應用於基於Concrete分佈的ADC量化器，假設感知放大器的雜訊是根據分佈，接著對雜訊分佈  與 建立機率模型，其中並且 ，對於雜訊分佈 ，雜訊模型假設為平均值為零的邏輯分佈（Logistic Distribution）且標準差以表示，可得到下列分佈 ，如圖3(a)所示。

基於上述假設，建立ADC雜訊模型，對於任意輸入訊號，能在每一個計算出對應的尾端機率，如圖3(a)的陰影區域，這些基於的尾端機率對於每一個代表位階的分類機率，如圖3(b)所示。本文建構每一個輸入ADC量化器的激勵函數訊號的分類機率，其中，，公式如下:

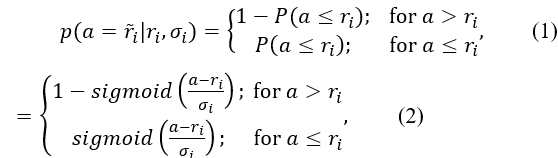
表示累積機率密度函數（Cumulative Distribution Function, CDP），將得到的分類機率標準化，透過上述分類機率的假設及建立，可以模擬感知放大器的量化雜訊，還能夠防止深度學習網路過度擬合。

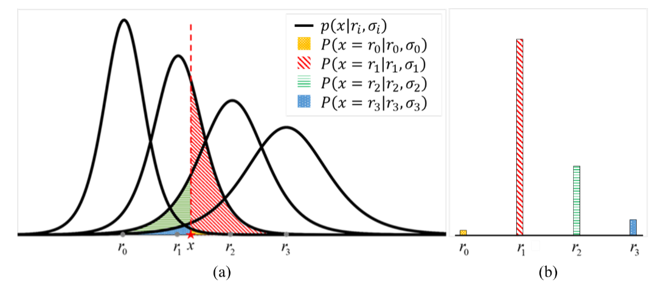
圖 3 提出的ADC量化流程 (a) 陰影區域表示在每個對應分布產生的尾端機率(b) 將基於的尾端機率作為x對於每一個代表位階的分類機率。

[4][5]介紹了基於重新參數化的量化演算法，其方法為引入Concrete分布取代分類分布(Categorical Distribution)，詳細如下: [4][5]介紹了基於重新參數化的量化演算法，其方法為引入Concrete分布取代分類分布(Categorical Distribution)，詳細如下:

表示從Concrete分布取出的隨機樣本，溫度常數控制近似的程度，也就是當，Concrete分布將會消退成分類分布。
綜上所述，本文提出基於Concrete分布的ADC量化器，完善能識別記憶體內類比混合運算電路限制的量化演算法。
 

實驗結果

• 實驗設置

實驗預設的位元數參數為2-2-32-V ，由左至右分別表示權重位元數、激勵函數位元數、ADC量化位元數、分群中的通道數量， 表示不採用分群卷積，ADC量化器的參數設定如下: 初始值根據輸入訊號最大及最小值決定，並除以;  值固定為0，確保量化代表位階保有0值，網路架構皆透過Adam[6]優化器訓練，學習率初始值設置為1e-4，透過Tensorflow[7]進行訓練。

CIFAR-10實驗採用VGG網路變體如下: 2x(16C)-MP-2x(32C)-MP-2x(64C)-MP-128FC-Softmax，總共訓練400個Epoch，每經過100個Epoch學習率會除以10，每個batch大小為100。

• 基於STE與Concrete分布的ADC量化器比較

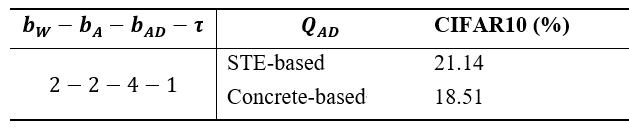
本節比較兩個ADC量化器，基於STE的ADC量化器與基於Concrete分布的ADC量化器，在CIFAR-10上做詳細的比較，如表1，Concrete分布的ADC量化器相較於傳統基於STE的ADC量化器能有更好的表現，結果顯示了在面對SRMP的問題時Concrete分布的ADC量化器測試CIFAR-10資料集能有2.63%的模型準確率提升。

表1 基於STE與Concrete分布的誤差測試結果

結論

本文提出了基於記憶體內類比混合運算的硬體規格的條件下，提出極小讀取邊際問題的機率模型，並使用重新參數化技巧結合所提出的機率模型，改進ADC量化器，使得具有感知放大雜訊適應性，所提出的基於Concrete分布的ADC量化器能提升2.63%的CIFAR-10準確率，能有效應用於多位元記憶體內類比混合運算的硬體。

參考資料

[1] P. Chi et al., "PRIME: A Novel Processing-in-memory Architecture for Neural Network Computation in ReRAM-based Main Memory", Int. Symp. On Comp. Arch., pp. 27-39, 2016.
[2] W. H. Chen et al., "A 65nm 1Mb nonvolatile computing-in-memory ReRAM macro with sub-16ns multiply-and-accumulate for binary DNN AI edge processors", IEEE ISSCC Dig. Tech. Papers, pp. 494-496, Feb. 2018.
[3] C.-X. Xue et al., "24.1 a 1Mb multibit ReRAM computing-in-memory macro with 14.6ns parallel MAC computing time for CNN based AI edge processors", Proc. 2019 IEEE Int. Solid-State Circuits Conf., pp. 388-390.
[4] J. Faraone, N. Fraser, M. Blott, P. H. Leong, "SYQ: Learning Symmetric Quantization for Efficient Deep Neural Networks", CVPR, 2018. [5] D. Zhang, J. Yang, D. Ye, G. Hua, "LQ-Nets: Learned quantization for highly accurate and compact deep neural networks", ECCV, 2018.
[6] D. P. Kingma, J. L. Ba, "Adam: A method for stochastic optimization", Proc. Int. Conf. Learn. Represent., pp. 1-41, 2015.
[7] M. Abadi, A. Agarwal et al., "Tensorflow: Large-scale machine learning on heterogeneous distributed systems", 2016.