資訊就是資產，安全多方運算能應用在保護客戶資料又能提供服務。「兩位富翁約在一間餐廳聚餐並商談合作。餐敘畢，按情理該由較有錢方買單才不致失禮，但兩位富翁並不知道誰較有錢，但又不願透露各自財產……」這是密碼學上知名的兩難問題，可由「信任第三方（trusted 3rd party）」－如餐廳經理出面解決：兩位富翁只須分別將財產總額透露給餐廳經理，餐廳經理即可公佈答案；但此問題的難處在於無法客觀地確認餐廳經理（或任何人）是否值得信任，也無法避免事後的「買通」。
此問題的技術性解法在1986年的一場IEEE會議中由台灣大學畢業的姚期智（Andrew Yao）先生首先提出，現今稱為混淆電路（Garbled Circuit），是「安全多方運算」的始祖；後來發明RSA加密法之其中一位大師Shamir提出以「秘密分享（Secret Sharing）」達成安全多方運算。由於此兩種手段皆可達到可確保使用者隱私的雲端「盲服務」－即服務提供者不須知道您的資料卻能為您服務，本文一步一步帶您探究竟。
安全多方運算的應用
愈來愈多人認同「資訊即資產（Information as an Asset）」，兩位富翁不願透露財富，是因這資訊可以成為商業上的利器；這和許多使用安全多方運算的應用動機是一樣的，其至少包含兩方以上不願透露各自隱私資料的個體，但卻又希望得到基於雙方資料的某運算結果。由應用來看可例舉如下表。
表１ 安全多方運算可能的應用
表中第1~5項的應用案例中，參與運算的個體各拿出對稱且同質的資料：雙方資料都是機密，不可透露給對方，但卻想得到運算的結果。而在第5~8項的例中，參與運算的一方是提供運算的服務者，另一方是提供資料的客戶：應用案例中服務者用於運算時的參數代表的是其know-how，不可告訴客戶，但客戶的資料同樣珍貴，亦不適用明文（plaintext）揭露予服務者。若依運算難度來看，安全多方運算的應用可如1~4項的簡單運算，亦或像5~8項較複雜的運算；但不論難易，上述應用「理論上」都可以用安全多方運算完成以取代「信任第三方」，達到「盲服務」的境界。
「盲服務」境界：對企業來說，第6應用案例若以安全多方運算實作，企業便不必養一群人做機密資料的分析，而是將企業的資料「混淆地」外包給專業資料分析公司，分析公司只能在混淆後的資料下「盲」運算解析出結論，可確保企業機密不外洩。再看另一應用案例，許多人常用的「語音轉成文字」服務：即將人聲傳到Google或Apple等公司，他們再以機械學習等技術轉成文字回傳，省去手機上打字的麻煩。不過，既然聲音可被轉成文字，那您的聲音當然也可被合成，甚至作為犯罪工具。若能運用安全多方運算實作此服務，服務者將只能取得您「如雜訊般」混淆語音便能轉出文字，避免您的聲音被濫用。這樣的公司（如[1]）提供的就是一種盲服務－相同的概念其實在學界已存在多年，只是近年來因全同態加密（Fully-Homomorphic Encryption; FHE）[2]技術的突破，受到矚目；不過值得注意的是，與全同態加密相比，安全多方運算的速度更快、「理論上」更易能實現各種運算。
為什麼是「理論上」？既然安全多方運算這麼行，為什麼市面上尚不見其應用服務火紅？要回答這問題，就先得要了解安全多方運算的基本原理。由於安全多方運算主要可由兩種做法實現，因此以下本文首先針對「混淆電路」進行介紹，有了概念後，再去了解「秘密分享」的作法，最後回過頭分析二種作法的優劣。
1.混淆電路
具工程背景的讀者大多知道「理論上」任何運算都可以由萬用邏輯閘（universal logic gate）如NAND所構成，因此只要能實作出任一「混淆」萬用邏輯閘，理論上就能進行任意「安全兩方運算」。是故，混淆電路的技巧的通用性只需以NAND邏輯閘證明。如圖一所示，若將NAND運算之雙方稱為Alice及Bob，假設輸入端x之值由Alice提供，輸入端y由Bob提供，「混淆NAND」可讓雙方在不提供各自的布林值下，正確地運算出下圖-真值表（truth table）中的z。
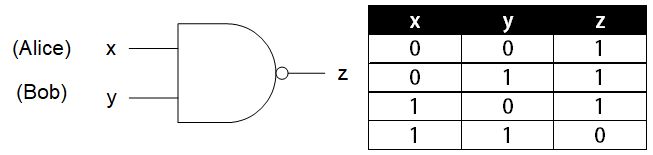圖1 NAND邏輯閘步驟一、Alice隱藏真實布林值：為了隱藏所有布林值，作為一位混淆者（Garbler）Alice首先為x、y、z分為產生代替0與1的亂數標籤（label），如下圖為例，在x上0的標籤為abcdef、1的標籤為ghijkl（請注意，本例中的亂數標籤具有規則性是為了說明概念；真正混淆電路的標籤是隨機亂數）；而y和z也各自有其不同的亂數標籤。因為標籤為隨機亂數，故只有Alice知道標籤與真實布林值的對應關係。假設Alice想將x值設為0，則在運算時，她只須把例子中的標籤abcdef交給Bob，而不必擔心該標籤透漏了x的值。
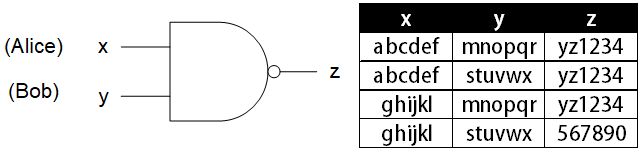圖2 隱藏真實數值後的AND邏輯閘步驟二、Alice產生「混淆真值表」並「洗牌」傳給Bob：如下圖所示，Alice將z欄中的各標籤用對應之x及y標籤作為金鑰，以任一對稱加密法Ekey（）進行雙層加密，內層的金鑰為y標籤，外層的金鑰為x標籤，得到混淆真值表（Garbled Truth Table; GTT），因為這四個欄位所使用的金鑰組合皆不同，因此就算z的布林值相同，其加密結果都是不同的。Alice將這個混淆真值表的z欄位「洗牌（shuffle）」後傳給Bob。假設沒有正確的標籤去解碼，這GTT對Bob來說只是四個不同的亂碼，且不具任何意義。
圖3 混淆真值表GTT
步驟三、Bob運算混淆真值表：如上圖右側所示，作為一位運算者（Evaluator），假設Bob取得了GTT和標籤abcdef，那麼他已能解碼第3和第4列的外層加密，但剩下來的內層加密保護必須向Alice取得Bob想要的標籤才能解碼。一個錯誤的做法是Bob直接向Alice說想要的y是1，則Alice給Bob標籤stuvwx後，Bob就能完成內層解碼，取出z的標籤zy1234；但這麼做Alice就知道Bob的值是1，破壞了隱私原則。為了在「Alice不能知道Bob的選擇」下讓Bob取得標籤，我們須借助「渾然不覺傳輸（Oblivious Transfer; O.T.）技術。
步驟四（Optional）、渾然不覺傳輸O.T.：O.T.旨在讓Bob取得Alice手邊的資料m0或m1（即例子中的標籤mnopqr或stuvwx），但不能讓Alice知道哪一個被取走。作為其中一個O.T.的可行做法，圖4以離散指數運算及對稱加密完成O.T.。其中，由於離散指數運算的反動作（discrete log）為NP-hard的難題，因此可確保Bob的選擇無法在「有效時間（如以超級電腦運算100年）」內被Alice推算出來。（請注意，並不是每一個GTT都需要進行O.T.，只有當標籤須由Alice那取得時才需要，因此步驟四為optional。）
步驟五、結算結果：當Bob取得標籤stuvwx，他就能順利完成內層解碼，取得z的標籤zy1234。但Bob並不知zy1234為何意，因此須將zy1234再傳回給Alice，由Alice查表後告知Bob結果（在此例中為布林值1）。如此雙方合作完成了所謂的「安全兩方運算」。
圖4 渾然不覺傳輸O.T.
1-1 多級混淆電路
混淆電路既稱為電路，一般都包含了多個邏輯閘。因此Bob取得z的標籤zy1234後，若後方還有其它邏輯閘的GTT，即可用該標籤繼續解碼下一級邏輯閘；若下一級的標籤都已準備好（如以透過前一級的運算結果或事前的O.T.取得），則Bob可直接透過解碼進行下一級的運算。如下圖所示，解密後的標籤可繼續作為下一級邏輯閘的解密金鑰，解出下一級的標籤，因此步驟一和步驟四的「標籤交換動作」一般只發生在整個運算的初始化時，一旦初始完成且所有的GTT都被傳給Bob，剩下的運算工作都是有Bob自己完成（所以稱其為Evaluator）。另外，如下圖中的問號所示，混淆電路的GTT並不會透露各邏輯閘的種類，因此在某種程度上還能保護電路設計。
圖5 混淆電路
由於「理論上」任何運算都可被描述為電路，因此混淆電路「理論上」能實作任何演算法，完成任何運算。舉例來說，AES加解密函式由於運算具規律性（regularity），已於被製作為混淆電路[3]，運算的雙方可在各持金鑰及明文（plaintext）而互不揭露的情形下，得到AES的密文（ciphertext）。
混淆電路的小問題：按上述混淆電路的基本原理，作為一位混淆者，Alice須對每個邏輯閘產生四個加密欄位，而這四個加密欄位都得傳給運算者Bob。若一個電路須用到10萬個邏輯閘，混淆者就得完成40萬次加密，以生出40萬個加密欄位，若每加密欄位為16位元組，則大約6MB的資料量須被傳送給Bob。而在解碼混淆電路時，運算者還須進行最多40萬次解密，才能完成一次安全兩方運算。也許按現今的網路頻寬和CPU效能來看，這雖然不是什麼大麻煩，但確實不是件輕鬆的工作，因此許多學者前仆後繼對混淆電路進行改良。
混淆電路的改良：三十多年的研究發現混淆電路以AND及XOR來實現的優點高過NAND。事實上研究顯示[4]，若運算只要用的XOR，則混淆者和運算者完成不用進行上述的加解密工作，達到free-XOR的效果；是故，混淆電路一般只須估算AND的數量，而AND的混淆電路運算也已被改良。舉例來說，透過point-and-permute的技巧[5]，運算者本來對一個AND需要四次解密，現在只須做一次；而透過row-reduction技巧[6]，混淆者本來一個AND需要四次加密，現在也可降為三次，若再在運用half-AND技巧[7]，可達到理論上最佳的兩次加密。這些改良與進步，雖對減少所需計算機算力有幫助，但難掩混淆電路的大麻煩。
混淆電路的大麻煩：一般來說有規律性的運算往往能被製作成電路，因此較容易改製成混淆電路；但大型的運算往往需要動態（dynamic）演算法運算，這樣的動態運算如何能被製作成電路？換句話說，「如何將任何程式改為成電路」才是混淆電路的大麻煩！
1-2 基於混淆電路的大型運算
為了解決大型運算，學界陸續都有提出對策，也曾有能將程式（如ANSI C）轉換為混淆電路的解法[8]，但其程式語法往往多有設限。舉例來說，為了將loop展開（unroll）成電路，許多解法會要求loop數是固定的，但這樣的限制卻導致許多演算法（如tree search）難以實作。因此如何將任意程式轉換成電路，確實是混淆電路的主要問題；但即便真有一個萬能編譯器能做出這轉換，其產生出來混淆電路勢必會因為loop（及function）展開的關係，電路大小十分驚人。
混合式混淆電路：針對這樣混淆電路轉換的困難，馬里蘭大學（University of Maryland）發展了一套稱為ObliVM的框架及其對應的編譯器。此編譯器並不直接程式轉為電路，而是只將程式中的計算部份轉為以Java描述之電路元件，但保留如loop、function及if-else等條件跳躍。換句話說，ObliVM可以說是一種混合混淆電路及高階程式語言的解法。舉例來說，其Java描述之電路元件在執行的過程中，會呼叫ObliVM框架中的混淆電路元件，runtime間運行上述所介紹的混淆電路動作，但遇到迴圈時，又會按條件進行跳躍。這樣的設計使得許多演算法得以實現，因此適合用來實做大型兩方安全運算。ObliVM編譯器產生之生成檔並非一般的執行檔，而是以Java class形式產生，以置入ObliVM框架中執行。
ObliVM的框架：如下圖所示，ObliVM的框架本身分為兩個主體，左邊交給Alice以混淆者身份執行，右邊給Bob以運算者身份執行。這兩個主體會執行上述編譯完成之Java class，但因執行身份之不同，其間Java描述之電路元件所呼叫的函式庫也會不同。 如下圖中的Inputs Labeling所示，ObliVM和原來的混淆電路一樣，一開始會讓Alice對所有輸入訊號進行隱藏真實數值，然後將Alice的所有輸入值對應的標籤交給Bob；最後再利用O.T.將Bob所選定輸入值對應之標籤交給Bob。在完成標籤傳遞後，就可進行編譯完的安全兩方運算。
圖6 混淆電路
ObliVM的邏輯運算：安全兩方運算可以很複雜，但為了方便說明，上圖假設編譯後的Java class只有三個邏輯閘。對於第一個邏輯閘XOR來說時，Alice和Bob實際上執行的是CircuitLib函式庫中的xor（），由於ObliVM採納free-XOR[4]的改良，xor（）可以簡單的對XOR的輸入標籤進行一般的bit-wise XOR運算，運算所得到之輸出標籤可直接用於後級邏輯閘。至於AND，ObliVM框架會在執行緒遇到它時，自動為Alice產生其GTT並傳送給Bob進行GTT的解碼。
ObliVM只產出夠用的GTT：由於採用程式與電路混合運行，ObliVM讓混淆電路的運作更有彈性。舉例來說，原始的混淆電路會要求Alice一次產生整個運算所需的所有GTT；但在ObliVM框架內，執行緒每遇一個AND邏輯閘才須產生一個GTT。這麼做的好處是Alice不須預先知道有多少迴圈須執行，便能產生出剛剛好夠用的GTT。另外，ObliVM要求Alice進行邏輯閘的同步運算，但目標不是取得運算結果，而是讓Alice隨時知道每一個邏輯閘輸出端「0的標籤」，以作為reference ground，來解碼出最後的程序結果（即Bob的某結果標籤若與Alice相同，則解讀為0，反之解讀為1）。具體來說，ObliVM基於「0 AND 0 = 0」及「0 XOR 0 = 0」的事實，讓Alice對每一個邏輯閘都用0的標籤進行運算，即可得到各邏輯閘輸出之「參考用」0標籤。因為此reference ground的關係，ObliVM的NOT邏輯閘的實做，反倒由混淆者Alice這端進行：即「反相（invert）」Alice手上的參考用0標籤即可達成。
其它ObliVM運用的技巧：雖然ObliVM基於混淆電路，但它卻運用了混淆電路以外的技巧來避免因混用高階語言而導致如instruction trace及memory trace的資訊洩漏（leakage）。以instruction trace為例，若有一個if-else區塊撰寫如圖7上半部，且若s是Bob（Alice）的隱私資料，則Alice（Bob）可單單觀察是那一個指令被執行即可推知s的值，那這隱私資料就等於是被洩漏了。為了避免此問題，ObliVM的編譯器若發現s是隱私資料時，會將程序編譯如圖7下半部；按此編譯結果，不論s的值為何，這五個指令都會執行到，因此Alice（Bob）無法靠執行的順序推知s的真正值。
圖7 ObliVM為避免不當instruction trace之得效轉換至於memory trace的部份，ObliVM利用Oblivious RAM[9]來避免惡意者透過觀察記憶體存取pattern，防止其推得另一方的隱私資料。採用諸如此類的技巧後，ObliVM就能允許一些常用的資料結構（如array等）的使用，以利設計大型安全兩方運算。
1-3 基於混淆電路的富翁問題解法
回到最初的富翁例子，「誰較有錢」的運算其實是一個簡單的「比較器（comparator）」，它可（在ObliVM框架在以程式方式）被描述出圖8左邊的簡單電路。在圖8中，若（A3, A2, A1, A0）及（B3, B2, B1,B0）分別可用表示富翁甲及富翁乙的0~15億美金（假設之財富範圍），將金額的二進位輸入按上述步驟取得亂數標籤後，富翁甲可產生如圖5A中右邊的混淆電路，並將電路交給富翁乙運算；最後運算所得出的亂數標籤會再傳回給富翁甲，查表得出結論。
圖8 富翁問題之混淆電路
2.秘密分享
所謂的秘密分享用資訊語言來說，就是將一個密鑰分成許多份額（share），然後分配給一些相關參與者，當這些（足夠的）參與者同時拿出各自的份額時可以重建出該密鑰。實際例子可想像（電影常出現）國家的重大武器（如核武），通常需要總統、副總統與國防部長三位中的兩位同時提供鑰匙才能啟用。一般來說，秘密分享基本做法是將一秘密s分成n個份額s1，s2，…，並滿足sn）若已知任意t個Si，t≤n，可輕易求出s；2）若已知t-1或更少數量的si，則無法求出 s。這樣的秘密分享也稱作是（t,n）門限（threshold）方案。概念主要是在1979年由Adi Shamir [10][12]與G. Blakley [11]所提出，但兩者的解決手法不太相同，Shamir提出的是以多項式函數為出發點，利用多項式函數求解以及Lagrange插值公式，來構成與解決門限方案；Blakley的做法則是利用線性幾何的投影法來解決門限方案。
2-1 Shamir秘密分享
Shamir的秘密分享提供可調整安全性強度的彈性，允許只需部分的份額就可還原原始數據，它是一種基於多項式的（t，n）門限值秘密分享方案，其中n是參與方數，t是門限值，並且 n > t ≥ 1的整數，此方法提供了一種將秘密數據s隱藏在隨機多項式常數項中的方法，每一個點就是ㄧ份秘密份額，如圖9所示。任何t個份額的組合都可使用Lagrange插值公式重建回原始數據，但任何少於t個份額無法透露秘密的任何訊息。此方案可分為秘密分配與秘密恢復兩階段：
秘密分配：首先選擇比s和n大的質數p，建立一個具有隨機係數 ri (1≤ i ≤ t-1 )的t-1次方多項式，並將秘密設置在常數項，f(0)= s，利用此多項式產生n 個share，si=f(i)，i＝1、2、…、n，i 值是唯一的不可重複，然後分配si給參與者Pi。
秘密恢復：要打開一個秘密s需要任何t個份額，並使用Lagrange插值公式來解出一多項式即可得到f(0)= s
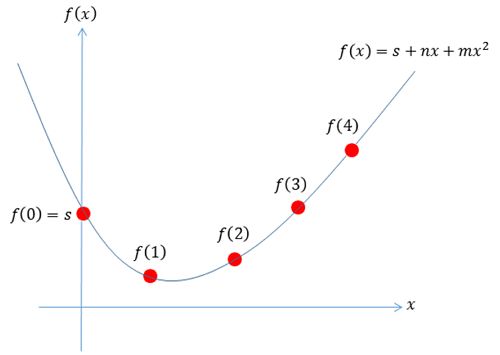圖9 Shamir秘密分享分拆秘密2-2 基於秘密分享的多方運算
安全多方運算主要是一群相互不信任的參與方在不洩露隱私下的共同計算，而秘密分享是資料分拆與重建的保護機密數據的技術，將秘密分享應用到安全多方運算，兩個技術的結合可以達到在不洩露隱私下完成所需的計算，利用秘密分享分拆原始資料並使用分拆後的資料進行運算例如相加或相乘，在將運算後的結果進行重建取得最後運算結果，運算過程中無需揭露任何私有資料。任何多方運算中的運算函式都可以通過一系列的加法和乘法組合來表示，所以我們需要做的就是要弄清楚如何將取到的份額進行相加和相乘。
加法運算（Addition）
假設有P1，P2，P3三方預進行總數加總，t=2，n=3，每一個Pi各建立一個具有隨機係數rk(1 ≤ k ≤ t-1)的t-1次方多項式fi(χ)，並將秘密放在常數項，三方使用相同索引參數α1、…、αn產生n個份額秘密分送給其他參與者si,j=pj。
每一個參與者Pi將接收到的各方第i部份的份額在本地執行加總計算。如圖10所示，在相同的坐標處上各方秘密份額的總和就是三方相加總和的秘密份額。也就是說每一方計算出來的值就總合值的其中一部分份額，將結果值發送給所有其他方Pi (1 ≤ j ≤ n)，這樣每一方都可得到總合的全部份額，
Pi 收集到的資料使用Lagrange插值公式來解出一新多項式即可得到f(0)=sum。
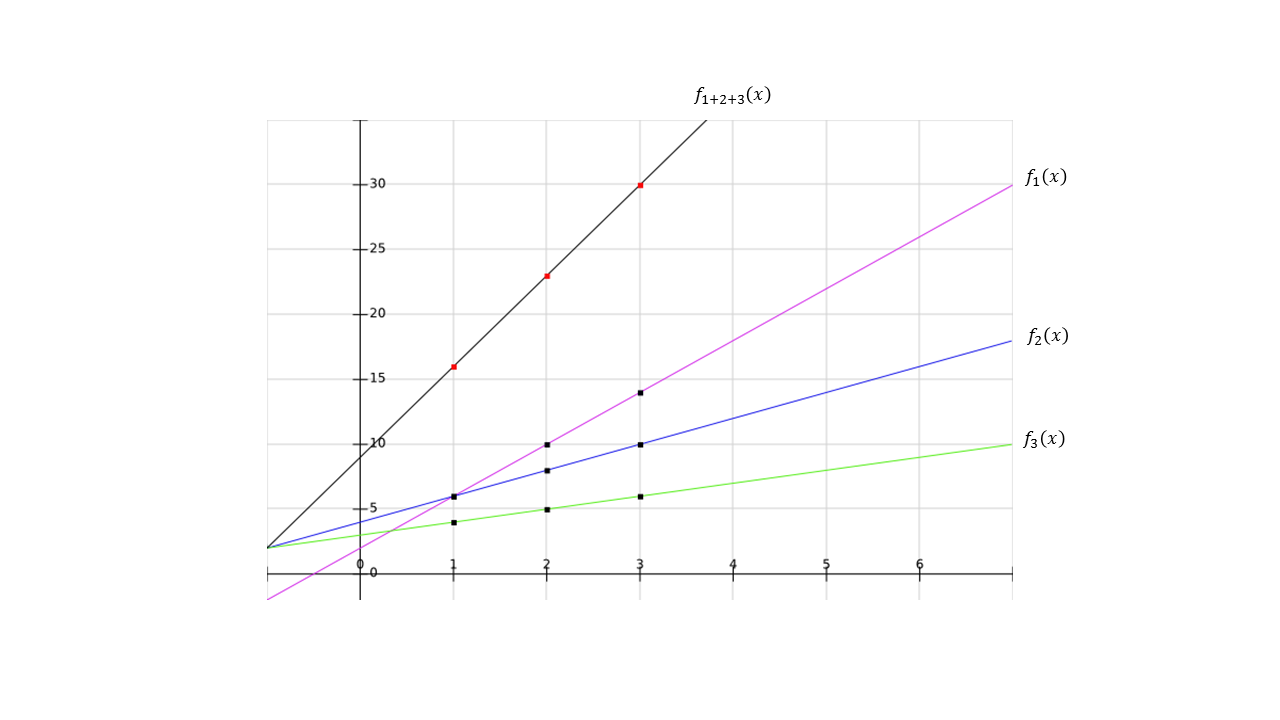圖10 三數相加產生新多項式乘法運算（Multiplication）
乘法並非如同加法那麼簡單，多方乘法計算需不斷執行兩方相乘，連續相乘結果將造成多項式變得太大，而太大的多項式產生出來的份額無法有足夠的參與者存儲，例如兩個秘密分別由兩個t次方多項式f(x)和g(x)分享，產生份額並進行乘法運算會得到具有次方多項式的秘密份額，在與一個秘密進行另一次乘法將產生4t次方多項式的秘密份額，以此類推每一次的相乘都會造成次方數倍數成長。為了克服這個問題，我們參考Gennaro、Rabin和Rabin的簡化乘法協議[13]，此協議是針對兩個相乘的多項式進行降幂，也就是說每一次兩方相乘，相乘結果的新多項式次方都會被降回原多相式的次方數但是常數項的乘積會被保留。假設有P1 ，P2 ，P3 三方預進行乘法運算，如同加法運算，各自建立一個隨機多項式並產生n個份額分送給其他參與者Pi (1 ≤ j ≤ n)。每一個參與者Pi 都會得到fi (χ)部份秘密份額fi (αi)，然後各參與者Pi 在本地進行f1 (αi)和f2 (αi)份額的相乘，並建立一個f1 (χ)與f2 (χ)和相同次方之隨機多項式hi (χ)將相乘的結果放在常數項，Pi 用新建立的多項式重新產生份額分配給其他參與者Pi (1 ≤ j ≤ n)，每一個Pi 會得到hi (j)部份份額，如圖11所示[14]，
每個參與者在將收到的份額用Lagrange多項式插值公式來解出一新多項式即可得到與f1 (αi)和f2 (αi)相同次方之f1 (αi)和f2 (αi)部份的相乘積
每個參與者Pi 將計算出來的相乘積在與f3 (αi)進行另一次的相乘，相乘的結果再分送給其他參與者Pi，每個參與者Pi用Lagrange多項式插值公式來解出一新多項式即可得到f(0)=三方相乘積。
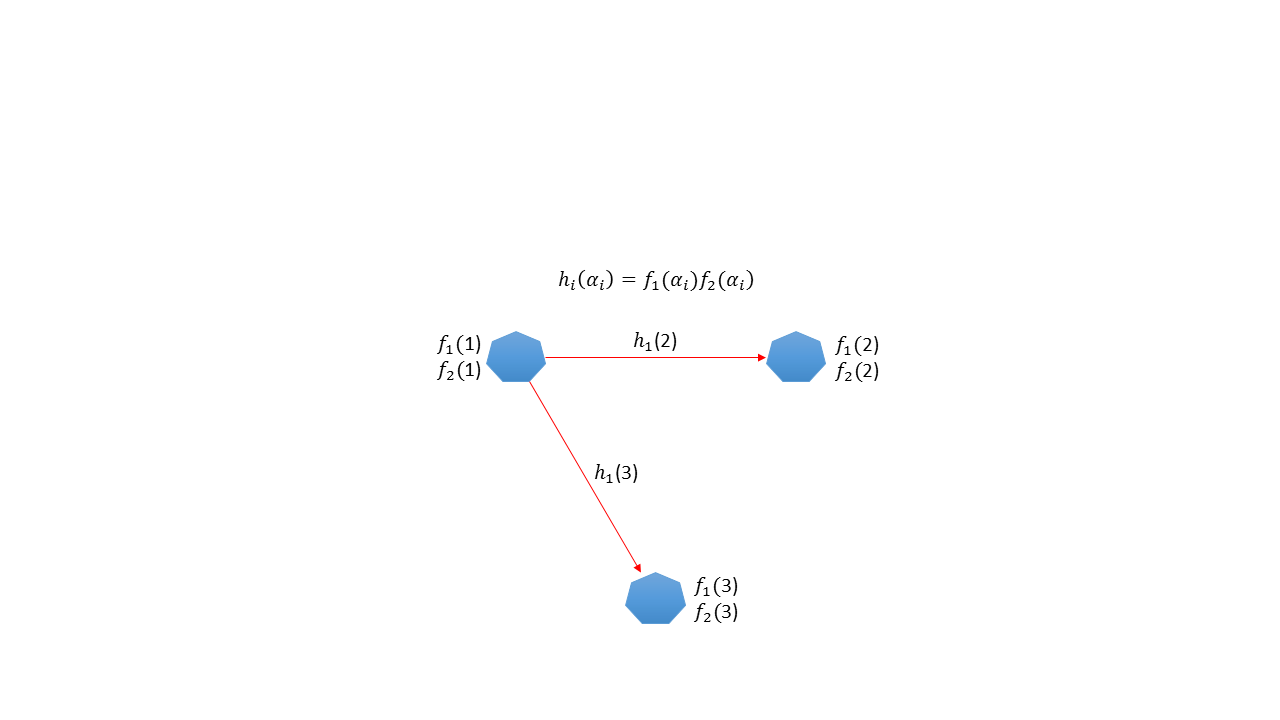圖11 多方進行兩數相乘2-3 基於秘密分享的富翁問題解法
讓我們再回到富翁問題，但這次利用秘密分享加法運算技術比較誰比較富有。透過祕密分享方法比較兩方誰比較富有，需借助第三方Charlie來做最後大小的判斷，其詳細步驟如下:
假設Alice財富是a，Bob的財富是b，Charlie為最後仲裁者，三方共同訂定一計算函數並對b取負數，c = a+（-b）；
- 步驟一 : Alice隨機建立一個具有隨機係數γk(1 ≤ k ≤ t-1)的t-1次方多項式，並將秘密放在常數項，產生3個份額秘密分送給其他參與者ai=Pi，Alice 得到a1、 Bob 得到a2和 Charlie得到a3 ;
- 步驟二 : Bob隨機建立一個具有隨機係數γk(1 ≤ k ≤ t-1)的t-1次方多項式，並將秘密放在常數項，產生3個份額秘密分送給其他參與者bi=Pi，Alice 得到b1、 Bob 得到b2和 Charlie 得到b3;
- 步驟三 : Alice、Bob和Charlie 各自將收到的部份資料進行計算ci=ai+(-bi) ；
- 步驟四 : Alice和Bob將計算的結果傳送給Charlie；
- 步驟五 : Charlie收到Alice 和 Bob 傳送過來的計算結果後，用Lagrange 多項式插值公式來求出一新多項式，f（0）=計算結果。Charlie無法從收到的數據得知原始的a和b值，但是，只要比較計算結果就可知道是誰比較富有，如果計算結果大於零則Alice比較富有，反之則Bob比較富有。而對於Alice和Bob來說，整個計算過程中都無法知道對方原始的數據；
- 步驟六：Charlie告訴Alice和Bob比較的結果。
3.混淆電路與秘密分享的比較
大致上來說，混淆電路適合安全「二」方運算，如上述之富翁問題，而又由於ObliVM的出現，混淆電路可應用於大型的編程運算。不過，若運算方的數算多於二，且運算主要由乘、加運算所構成，則極適合由秘密分享來實做。可惜，由於秘密分享目前尚無像ObliVM之運算框架支援，對於大型的編程運算必須手工製作，因此目前大型編程運算可能還是會以混淆電路為主。以目前的技術發展來看，混淆電路並沒能完全取代秘密分享，反倒若能將這二種做法合併使用，將可望對安全多方運算建立更大的應用可能性。
最具潛力實作成雲端「盲服務」-安全多方運算
在現代這個由資訊驅動的環境中，我們每天都會與大量的人/單位/系統/服務互動溝通，但這其中存在許多我們從未接觸過，並且與我們有利益上衝突、或是想竊取我們個人資料以從中得利的對象，若我們無法確認這些互動溝通對像是值得信任的，那該如何處理個人的隱私資料呢？我們不可能將所有敏感資料都存放在一個無人可取得的安全環境中，因為個人資料之所以有價值，是因為我們將它用來做一些事。因此，思考點應該在於，可以用什麼方式來控制與降低敏感資料在儲存、溝通、計算時的資訊洩漏。 安全多方運算可在實際數據不透露的條件下，完成多方間的協同分析（約定函數值計算），此特性打破傳統上大家認為數據計算一定要先處理資料數據的匯整；目前已有研究人員將安全多方運算的概念跟近期最火熱的分散式系統－區塊鏈結合，改善原本像Zcash雖然解決了隱私數據保護的問題，但卻沒有鏈上計算能力的缺點。安全多方運算能同時滿足數據流動與協同分析的需求，在應用上可切入金融、製造、醫療等對數據隱私相當重視的產業，例如金融業的信用徵信可廣納保險、醫療、物流等資訊，同時維護資料方的資訊保密性，促使數據資訊發揮最大的價值。 另一方面由於雲端服務的崛起，大量的資料都向雲端送去。這樣的趨勢對使用者來說提升了便利性，並為服務提供者解決了軟體盜版的問題；但這樣看起來雙贏的局面，其實還是隱含了危機。由於大量送往雲端的資料中不乏有機敏資料，以資安的角度來看，使用者的隱私其實是完全不存在的。而安全多方運算，是有潛力能被實作成雲端「盲服務」，在使用者享受雲服務的同時，可確保使用者的隱私資料不外洩。
參考文獻
[1] Technicolor, [Online], https://www.technicolor.com/
[2] Fully-Homomorphic Encryption, [Online]. https://en.wikipedia.org/wiki/Homomorphic_encryption
[3] Benny Pinkas, Thomas Schneider, Nigel P. Smart, and Stephen C. Williams. Secure two-party computation is practical. In Mitsuru Matsui, editor, ASIACRYPT 2009, volume 5912 of LNCS, pages 250–267. Springer, Heidelberg, December 2009.
[4] V. Kolesnikov and T. Schneider, “Improved garbled circuit: Free xor gates and applications,” in Automata, Languages and Programming. Springer, 2008, pp. 486-498
[5] D. Beaver, S. Micali, and P. Rogaway. The round complexity of secure protocols. In Proceedings of the twenty-second annual ACM symposium on Theory of computing, pages 503–513. ACM, 1990.
[6] Moni Naor, Benny Pinkas, and Reuban Sumner. Privacy preserving auctions and mechanism design. In Proceedings of the 1st ACM Conference on Electronic Commerce, EC ’99, pages 129–139, New York, NY, USA, 1999. ACM.
[7] Samee Zahur, Mike Rosulek, and David Evans. Two halves make a whole. In Advances in Cryptology-EUROCRYPT 2015, pages 220–250. Springer, 2015.
[8] N. Büscher, D. Kretzmer, A. Jindal, and S. Katzenbeisser. 2016. Scalable secure computation from ANSI-C. In WIFS.
[9] X. S. Wang, T.-H. H. Chan, and E. Shi, “Circuit ORAM: On Tightness of the Goldreich-Ostrovsky Lower Bound,” Cryptology ePrint Archive, Report 2014/672, 2014.
[10] A. Shamir. How to share a secret. Communications of the ACM, 22（11）:612–613, 1979.
[11] G. R. Blakley. Safeguarding cryptographic keys. In Proceedings of the National Computer Conference 48, pages 313–317, 1979.
[12] Strange L. From and Thomas Jakobsen. Secure Multi-Party Computation on Integers. Master’s thesis, University of Aarhus, 2006.
[13] GENNARO, R., RABIN, M. O., AND RABIN, T. Simplified vss and fasttrack multiparty computations with applications to threshold cryptography. In PODC '98: Proceedings of the seventeenth annual ACM symposium on Principles of distributed computing （New York, NY, USA, 1998）, ACM Press, pp. 101-111.
[14] Secret Sharing DAOs: The Other Crypto 2.0. [Online]. Available: https://blog.ethereum.org/2014/12/26/secret-sharing-daos-crypto-2-0/
相關連結: 回176期Cyber Cecurity專輯
